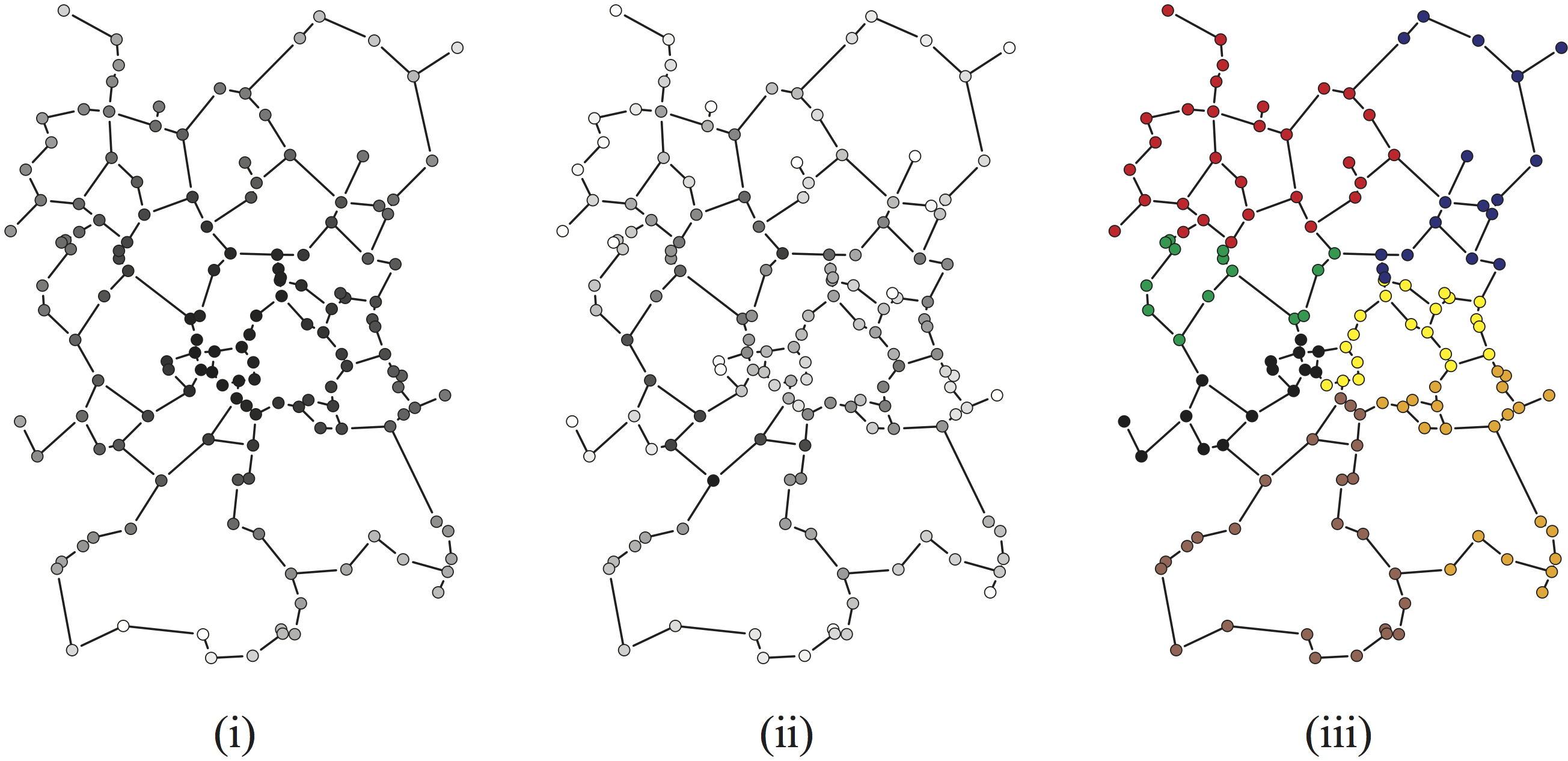
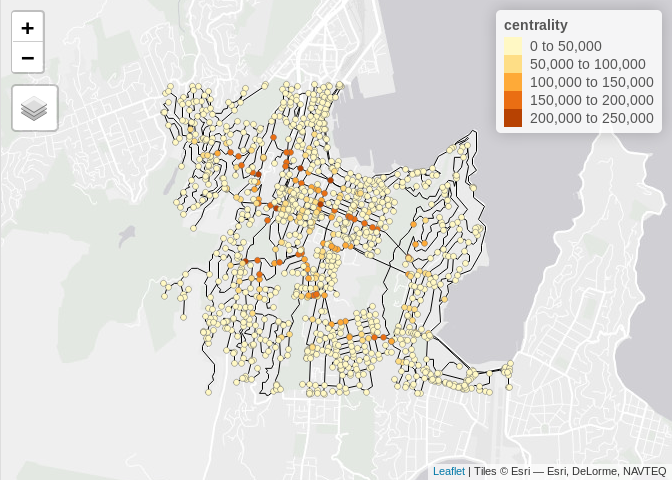
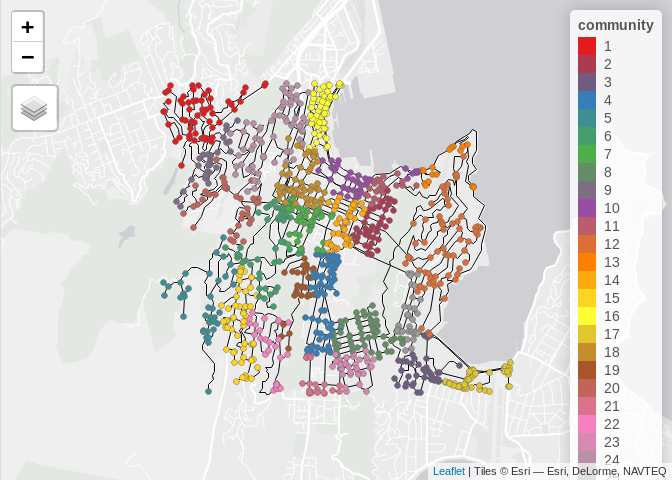
Extras
Storing the ‘previous’ node from which shortest path connection
was made to allows back-tracing of any required shortest path
Often, heuristics are applied to narrow the search, for example
not allowing the shortest path to deviate too far from a straight line connecting source
and target nodes
A popular alternative algorithm is called A*